Trong thế giới tài chính, chúng ta thường nghe về những mô hình kinh điển như CAPM, mô hình định giá quyền chọn Black-Scholes, hay những phương pháp quản lý rủi ro như Value at Risk (VaR). Nhưng ít ai biết rằng, đằng sau những công cụ này là một cuộc cách mạng toán học lặng lẽ được khởi xướng bởi một nhà toán học Nhật Bản vào những năm 1940. Đó là Kiyosi Itō, người đã phát triển một lĩnh vực toán học hoàn toàn mới – giải tích Itō – để mô hình hóa sự ngẫu nhiên. Không chỉ thay đổi cách chúng ta hiểu về xác suất và các quá trình ngẫu nhiên, giải tích Itō còn trở thành ngôn ngữ trung tâm của tài chính định lượng, giúp con người có thể mô hình hóa những biến động thị trường một cách chính xác hơn bao giờ hết.

Vấn đề lớn: Khi toán học cổ điển bất lực trước sự ngẫu nhiên

Trước khi có giải tích Itō, các nhà toán học và kinh tế học gặp phải một thách thức lớn: làm thế nào để mô hình hóa các chuyển động ngẫu nhiên như giá cổ phiếu hay lãi suất? Toán học cổ điển, vốn dựa trên các phương trình vi phân thông thường, yêu cầu các hàm phải có đạo hàm tại mọi điểm. Tuy nhiên, điều này lại không đúng với nhiều quá trình ngẫu nhiên trong thực tế. Một ví dụ điển hình là chuyển động Brown – mô hình miêu tả đường đi ngẫu nhiên của một hạt trong chất lỏng và sau này được ứng dụng rộng rãi trong tài chính. Các đường đi của chuyển động Brown có đặc điểm là liên tục nhưng không khả vi – nghĩa là chúng không có đạo hàm tại bất kỳ điểm nào. Điều này khiến cho các công cụ vi phân cổ điển trở nên vô dụng khi muốn phân tích các hệ thống có yếu tố ngẫu nhiên.

Giải pháp: Sự ra đời của giải tích Itō

Đối diện với vấn đề này, Itō đã phát triển một bộ công cụ toán học hoàn toàn mới để xử lý các quá trình ngẫu nhiên. Công trình của ông đặt nền móng cho giải tích Itō, một lĩnh vực toán học cho phép tính toán và phân tích các quá trình ngẫu nhiên phức tạp. Trọng tâm của giải tích này là bổ đề Itō (Itō Lemma), một quy tắc vi phân đặc biệt giúp tính toán đạo hàm của một hàm theo một quá trình ngẫu nhiên. Nếu trong giải tích cổ điển, chúng ta có quy tắc chuỗi của Leibniz, thì trong thế giới của các quá trình ngẫu nhiên, bổ đề Itō đóng vai trò tương tự. Công thức của bổ đề Itō có dạng:

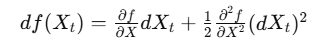
Điểm đặc biệt là thành phần thứ hai trong công thức này – phần bù cho sự ngẫu nhiên – không xuất hiện trong phép tính vi phân cổ điển. Điều này giúp các nhà nghiên cứu có thể làm việc với những chuyển động không khả vi mà vẫn giữ được các tính chất toán học quan trọng.

Từ toán học thuần túy đến cuộc cách mạng tài chính

Điều thú vị là Itō không hề có ý định tạo ra một cuộc cách mạng tài chính. Ông nghiên cứu về các quá trình ngẫu nhiên thuần túy từ góc độ toán học mà không hề nghĩ rằng công trình của mình sẽ có ứng dụng thực tiễn rộng lớn. Suốt nhiều thập kỷ, những công trình của Itō chỉ được biết đến trong giới toán học xác suất. Tuy nhiên, vào những năm 1970, các nhà kinh tế học như Robert Merton và Fischer Black đã nhận ra rằng công cụ của Itō chính là chìa khóa để mô hình hóa các quá trình tài chính. Họ đã sử dụng giải tích Itō để phát triển mô hình Black-Scholes – một trong những mô hình quan trọng nhất trong tài chính định lượng. Mặc dù bản thân Itō không trực tiếp tham gia vào sự phát triển của mô hình này, nhưng không thể phủ nhận rằng nếu không có giải tích Itō, các mô hình tài chính hiện đại sẽ không thể tồn tại.

Ứng dụng của giải tích Itō trong tài chính hiện đại

Ngày nay, giải tích Itō có mặt ở khắp nơi trong tài chính. Một số ứng dụng quan trọng bao gồm:

1. Mô hình hóa giá cổ phiếu và tài sản tài chính: Giải tích Itō là nền tảng cho mô hình chuyển động Brown hình học (Geometric Brownian Motion - GBM), một mô hình phổ biến để mô phỏng giá cổ phiếu.
2. Mô hình hóa lãi suất: Các mô hình như Vasicek, Cox-Ingersoll-Ross (CIR), và Hull-White đều dựa vào giải tích Itō để mô phỏng sự biến động của lãi suất theo thời gian.
3. Quản lý rủi ro tài chính: Các phương pháp đo lường rủi ro như Value at Risk (VaR), Expected Shortfall (CVaR) đều sử dụng các mô hình ngẫu nhiên để ước tính khả năng tổn thất của danh mục đầu tư.
4. Phương trình vi phân ngẫu nhiên (SDEs): Giải tích Itō là công cụ chính để giải quyết các phương trình vi phân ngẫu nhiên – loại phương trình mô tả nhiều hiện tượng trong tài chính, từ biến động giá cổ phiếu đến dao động lãi suất và sự lan truyền rủi ro trong hệ thống tài chính.

Di sản của một nhà toán học thầm lặng

Dù không được nhiều người biết đến như Black hay Merton, nhưng tầm ảnh hưởng của Itō đối với tài chính hiện đại là không thể phủ nhận. Ông không phải là một nhà tài chính, cũng không hề có ý định cách mạng hóa ngành tài chính. Nhưng những gì ông để lại đã giúp thế giới tài chính có một ngôn ngữ toán học hoàn chỉnh để mô hình hóa rủi ro và sự bất định. Trong một thế giới mà mọi thứ đều có yếu tố ngẫu nhiên, từ biến động giá tài sản đến các cú sốc kinh tế, di sản của Itō vẫn tiếp tục sống mãi.

Hơn nửa thế kỷ sau, những công cụ mà Itō phát triển vẫn là xương sống của ngành tài chính định lượng. Và nếu bạn là một nhà giao dịch, một nhà quản lý danh mục, hay một chuyên gia tài chính định lượng, thì dù trực tiếp hay gián tiếp, bạn vẫn đang sử dụng những ý tưởng mà Kiyosi Itō đã khai phá.

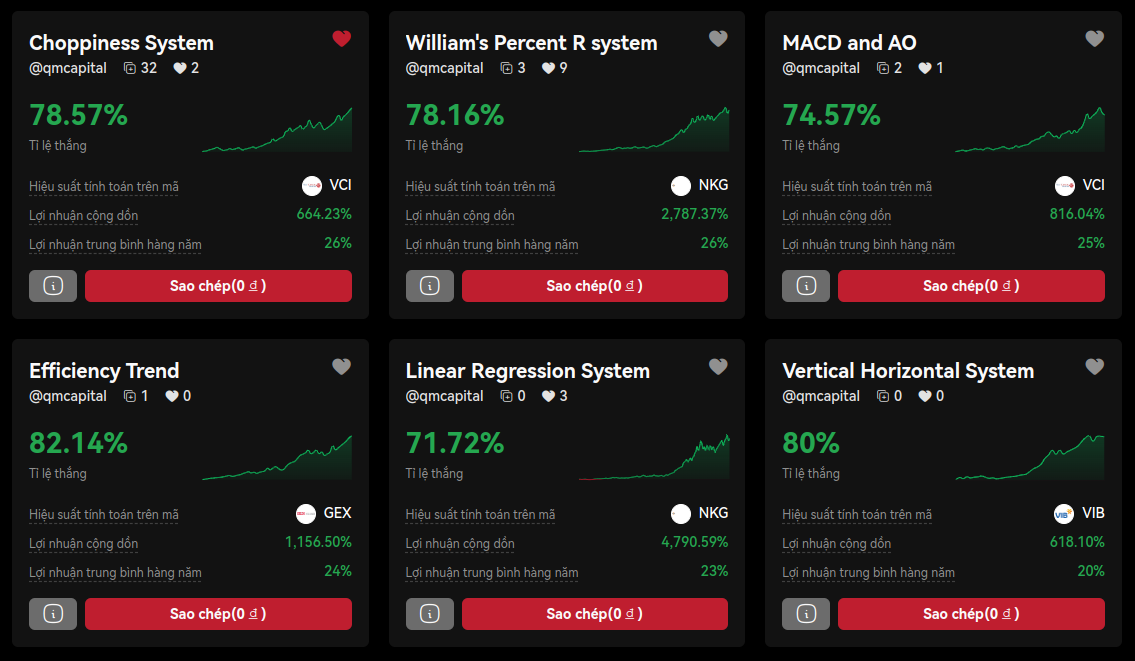
Hãy xây dựng và kiểm thử chiến lược giao dịch phái sinh của bạn trên nền tảng QMTRADE trước khi sử dụng tiền thật để tránh những rủi ro không đáng có.