Trang chủ
/ Kiến thức chung
/ [P1] Tổng hợp các phương pháp đánh giá rủi ro và hiệu suất trong đầu tư

[P1] Tổng hợp các phương pháp đánh giá rủi ro và hiệu suất trong đầu tư

19/04/2024

11,893 lượt đọc

Quản lý rủi ro trong tài chính là quá trình nhận diện, đánh giá và điều phối nguồn lực để kiểm soát rủi ro và giảm thiểu tác động của các biến cố bất ngờ. Đây là yếu tố then chốt để đảm bảo các chiến lược đầu tư an toàn và bảo vệ doanh nghiệp cũng như các bên liên quan khỏi rủi ro tài chính. Trong loạt bài này, QM Capital sẽ giới thiệu và phân tích chi tiết 5 phương pháp đánh giá rủi ro hiệu quả bằng Python, bao gồm Tỷ lệ Sharpe, Tỷ lệ Sortino, Tỷ lệ Omega, Tỷ lệ Calmar và Tỷ lệ Sụt giảm tối đa. Những công cụ này là thiết yếu cho nhà đầu tư, nhà phân tích tài chính và nhà khoa học dữ liệu để nâng cao hiệu quả trong quản lý rủi ro và đầu tư.

1. Tỷ lệ Sharpe

1.1. Khái niệm

Tỷ lệ Sharpe là một thước đo xem lợi nhuận thu được là bao nhiêu trên một đơn vị rủi ro khi đầu tư vào một tài sản hay đầu tư theo một chiến lược kinh doanh.

Tỷ lệ Sharpe được phát triển bởi William F. Sharpe và được sử dụng để giúp các nhà đầu tư hiểu được lợi tức của khoản đầu tư so với rủi ro của nó. Tỷ lệ này là lợi nhuận trung bình kiếm được vượt quá lợi nhuận phi rủi ro trên mỗi đơn vị rủi ro.

Cách thức hoạt động của Tỷ lệ Sharpe:

Nhà đầu tư thường xuyên đối mặt với hai mục tiêu mâu thuẫn: một là tối đa hóa lợi nhuận từ các khoản đầu tư, hai là giảm thiểu rủi ro, tức là giảm thiểu khả năng thua lỗ.

Tỷ lệ Sharpe được sử dụng để cung cấp cho nhà đầu tư một chỉ số đánh giá hiệu quả đầu tư đã điều chỉnh theo rủi ro. Tỷ lệ Ratio có thể áp dụng để phân tích hiệu suất quá khứ hoặc kỳ vọng hiệu suất tương lai, nhưng trong cả hai trường hợp, tỷ lệ tài chính quan trọng này giúp nhà đầu tư hiểu liệu lợi nhuận có đến từ quyết định thông minh hay chỉ là chấp nhận quá nhiều rủi ro. Nếu là trường hợp sau, nhà đầu tư có thể sẽ chịu tổn thất lớn hơn mức họ có thể chấp nhận nếu thị trường biến động bất lợi.

Tỷ lệ Sharpe được tính bằng cách lấy lợi nhuận vượt trội của một tài sản hoặc danh mục đầu tư trong một khoảng thời gian xác định, sau đó chia cho độ lệch chuẩn của danh mục đó, đây là thước đo của mức độ biến động. Độ lệch chuẩn càng cao thì mức độ rủi ro càng lớn, và ngược lại, tỷ lệ Sharpe càng cao cho thấy mức độ hiệu quả rủi ro càng tốt

Công thức tính:

Tỉ lệ Sharpe = (Rp – Rf)/ σp

Trong đó:

Rp là tỷ suất lợi nhuận của danh mục đầu tư

Rf là tỷ suất lợi nhuận phi rủi ro

σp là độ lệch chuẩn của tỷ suất lợi nhuận vượt quá của danh mục

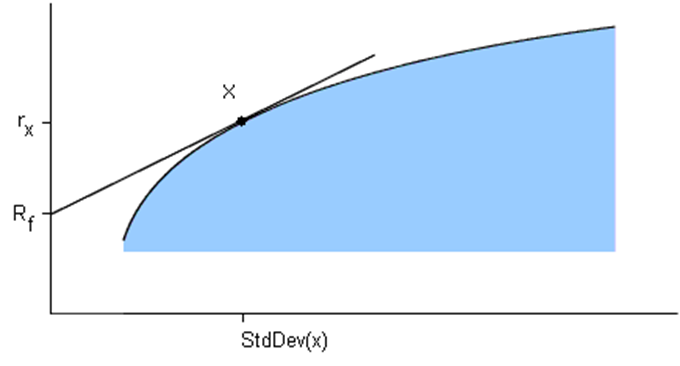
1.2. Đặc điểm

Tỷ lệ Sharpe là công cụ đo lường hiệu quả lợi nhuận điều chỉnh theo rủi ro được sử dụng phổ biến trong ngành tài chính. Theo Lý thuyết Danh mục Đầu tư hiện đại (Modern Portfolio Theory - MPT), việc bổ sung các tài sản có mối tương quan thấp vào một danh mục đầu tư đa dạng có thể giúp giảm thiểu rủi ro mà không làm giảm lợi nhuận kỳ vọng.

Giả định rằng rủi ro tương đương với mức độ biến động của lợi nhuận, một danh mục đầu tư (DMĐT) đa dạng hóa cao sẽ có Tỷ lệ Sharpe cao hơn so với những danh mục ít đa dạng hơn.

Tỷ lệ Sharpe không chỉ được áp dụng để phân tích hiệu suất quá khứ của danh mục đầu tư (Ex-Post), mà còn có thể sử dụng để ước tính hiệu suất tương lai thông qua Tỷ lệ Sharpe dự kiến (Ex-Ante). Điều này được thực hiện bằng cách sử dụng lợi nhuận thực tế đã đạt được và so sánh với mức lợi nhuận không rủi ro để xem xét hiệu quả đầu tư dưới góc độ điều chỉnh rủi ro.

Tỷ lệ Sharpe cho phép nhà đầu tư:

So sánh tỷ lệ rủi ro/lợi nhuận của các tùy chọn đầu tư khác nhau.
Đánh giá hiệu quả của các chiến lược trong một lựa chọn đầu tư duy nhất (tỷ lệ rủi ro/lợi nhuận của các danh mục đầu tư, advisor khác nhau, v.v.).
Chọn một chiến lược hấp dẫn hơn về mặt giảm thiểu rủi ro với cùng một mức lợi nhuận.

1.3. Ví dụ về tỷ lệ Sharpe

Xem xét hai danh mục đầu tư: Danh mục A dự kiến sẽ mang lại lợi nhuận 14% trong vòng 12 tháng tới, trong khi Danh mục B dự kiến sẽ mang lại lợi nhuận 11% trong cùng kỳ.

Nếu không xét đến rủi ro, rõ ràng Danh mục A là lựa chọn ưu việt hơn dựa trên mức lợi nhuận đơn thuần.

Nhưng liệu rủi ro. Đây là lúc mà tỷ lệ Sharpe cung cấp một cái nhìn toàn diện hơn về khoản đầu tư. Trong ví dụ này, Danh mục A có độ lệch chuẩn 8% (rủi ro cao hơn) và Danh mục B có độ lệch chuẩn 4% (rủi ro thấp hơn). Lãi suất không rủi ro là 3%, là lợi tức của trái phiếu chính phủ Mỹ có kỳ hạn trung bình.

Tỷ lệ Sharpe cho mỗi danh mục:

Danh mục A: (14 - 3) / 8 = Tỷ lệ Sharpe là 1.38

Danh mục B: (11 - 3) / 4 = Tỷ lệ Sharpe là 2

Với mức độ biến động cao hơn được tính vào Danh mục A, tỷ lệ Sharpe của nó thấp hơn so với của Danh mục B. Điều này biết rằng với tỷ lệ Sharpe là 2, Danh mục B mang lại lợi nhuận tốt hơn trên cơ sở điều chỉnh rủi ro.

=> Một tỷ lệ Sharpe nằm giữa 1 và 2 được coi là tốt. Tỷ lệ từ 2 đến 3 là rất tốt, và bất kỳ kết quả nào cao hơn 3 đều được đánh giá là xuất sắc.

1.4. Phân tích tỷ lệ Sharpe hàng năm của Apple bằng Python

import pandas as pd

import numpy as np

import yfinance as yf

import matplotlib.pyplot as plt

tickerSymbol = ‘AAPL’

tickerData = yf.Ticker(tickerSymbol)

tickerDf = tickerData.history(period='1d', start='2012-1-1')

tickerDf['returns'] = tickerDf['Close'].pct_change()

# Annualized Sharpe Ratio

rolling_sharpe = np.sqrt(252) * tickerDf['returns'].rolling(252).mean() / tickerDf['returns'].rolling(252).std()

plt.figure(figsize=(15,7))

ax1 = plt.gca()

ax1.plot(rolling_sharpe, label='Rolling Sharpe Ratio', linewidth=1.5)

ax1.axhline(y=1, color='red', linestyle='--', label='Good Sharpe Ratio Threshold: 1')

ax1.set_title('Rolling 1-Year Sharpe Ratio with Stock Price', fontsize=16)

ax1.set_ylabel('Sharpe Ratio', fontsize=14)

ax1.legend()

ax2 = ax1.twinx()

ax2.plot(tickerDf['Close'], color='grey', alpha=0.3, label='Stock Price')

ax2.set_ylabel('Stock Price', fontsize=14)

plt.tight_layout()

plt.show()

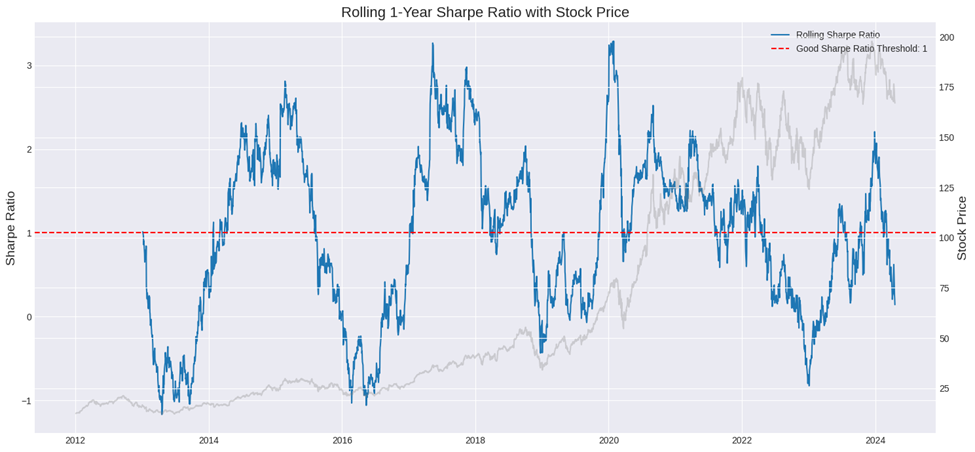
Ví dụ Phân tích tỷ lệ Sharpe hàng năm của Apple bằng Python

2. Tỷ lệ Sortino

2.1. Khái niệm

Tỷ lệ Sortino là một biến thể của Tỷ lệ Sharpe, được sử dụng để đo lợi nhuận điều chỉnh theo rủi ro của danh mục đầu tư bằng cách so sánh hiệu suất với độ lệch chuẩn rủi ro đi xuống, thay vì độ lệch chuẩn tổng thể của lợi nhuận danh mục

Công thức tính Tỷ lệ Sortino là:

Tỷ lệ Sortino = (Rp – rf)/σd

Trong đó:

Rp là lợi nhuận danh mục đầu tư thực tế hoặc dự kiến

rf là lãi suất phi rủi ro

σd là độ lệch chuẩn của rủi ro thua lỗ

Tỷ lệ Sortino là một công cụ đánh giá hiệu suất đầu tư rất có giá trị đối với nhà đầu tư, nhà phân tích và người quản lý danh mục đầu tư. Tỷ lệ này chỉ tính đến độ lệch chuẩn của các lợi nhuận âm, tức là chỉ xem xét rủi ro đi xuống, làm cho nó trở thành một công cụ đo lường rủi ro một cách chính xác hơn so với các phương pháp truyền thống như tỷ lệ Sharpe, vốn xem xét biến động tổng thể. Điều này rất quan trọng vì biến động lợi nhuận tích cực là có lợi cho nhà đầu tư và không nên được coi là một yếu tố rủi ro.

2.2. Ví dụ về tỷ lệ Sortino

Cũng giống như tỷ lệ Sharpe, giá trị tỷ lệ Sortino càng cao càng tốt. Khi xem xét hai khoản đầu tư tương tự nhau, một nhà đầu tư hợp lý sẽ thích một khoản đầu tư có tỷ lệ Sortino cao hơn bởi vì điều đó có nghĩa là khoản đầu tư đang kiếm được nhiều tiền lãi hơn trên mỗi đơn vị rủi ro xấu mà nó phải chịu.

Ví dụ: Giả sử Quỹ tương hỗ X có tỷ lệ hoàn vốn hàng năm là 12% và độ lệch rủi ro thua lỗ là 10%. Quỹ tương hỗ Z có lợi nhuận hàng năm là 10% và độ lệch rủi ro thua lỗ là 7%. Tỷ lệ lãi suất phi rủi ro là 2.5%. Tỷ lệ Sortino cho cả hai quỹ sẽ được tính như sau:

Tỷ lệ Sortino của Quỹ tương hỗ X = (12% - 2.5%)/ 10% = 0.95

Tỷ lệ Sortino của Quỹ tương hỗ Z = (10% - 2.5%)/ 7% = 1.07

Mặc dù Quỹ tương hỗ X có Tỷ suất lợi nhuận cao hơn 2%, nhưng nó không kiếm được lợi nhuận đó hiệu quả như Quỹ tương hỗ Z, chứng minh bởi các độ lệch rủi ro thua lỗ của họ. Dựa trên kết quả này, Quỹ tương hỗ Z là lựa chọn đầu tư tốt hơn.

Mặc dù tỷ lệ lợi nhuận phi rủi ro được sử dụng phổ biến hơn, các nhà đầu tư vẫn có thể sử dụng lợi nhuận kỳ vọng trong tính toán. Để giữ cho công thức được chuẩn xác, nhà đầu tư nên nhất quán sử dụng một loại lợi nhuận.

2.3. Phân tích tỷ lệ Sortino hàng năm của Invesco QQQ Trust (QQQ) bằng Python

import pandas as pd

import numpy as np

import yfinance as yf

import matplotlib.pyplot as plt

# Fetch Data

tickerSymbol = "QQQ"

tickerData = yf.Ticker(tickerSymbol)

tickerDf = tickerData.history(period='1d', start='2010-1-1')

tickerDf['returns'] = tickerDf['Close'].pct_change()

MAR = 0 # Minimum Acceptable Return

# Sortino Ratio calculation

sortino_ratio = tickerDf['returns'].rolling(252).apply(lambda x: np.mean(x - MAR) / np.sqrt(np.mean(np.minimum(0, x - MAR)**2)))

threshold = sortino_ratio.mean()

# Aesthetics

plt.figure(figsize=(15, 7))

plt.style.use('seaborn-darkgrid')

palette = plt.get_cmap('Set1')

# Plot Sortino Ratio

ax1 = plt.gca()

ax1.plot(sortino_ratio.index, sortino_ratio, color=palette(0), linewidth=1.5, label='Sortino Ratio')

# Smoothened Sortino Ratio with a moving average

ax1.plot(sortino_ratio.index, sortino_ratio.rolling(window=252).mean(), color='orange', linestyle='--', label='1-Year MA')

ax1.axhline(y=threshold, color='red', linestyle='--', label=f'Threshold (Mean: {threshold:.2f})')

# Aesthetics for Sortino Ratio

ax1.set_ylabel('Sortino Ratio', fontsize=14, color=palette(0))

ax1.legend(loc='upper left')

ax1.set_title(f'Rolling 1-Year Sortino Ratio with Stock Price (MAR: {MAR*100}%)', fontsize=16)

# Stock Price Plot on secondary y-axis

ax2 = ax1.twinx()

ax2.plot(tickerDf.index, tickerDf['Close'], color=palette(1), alpha=0.4, label='Stock Price')

ax2.set_ylabel('Stock Price', fontsize=14, color=palette(1))

plt.tight_layout()

plt.show()

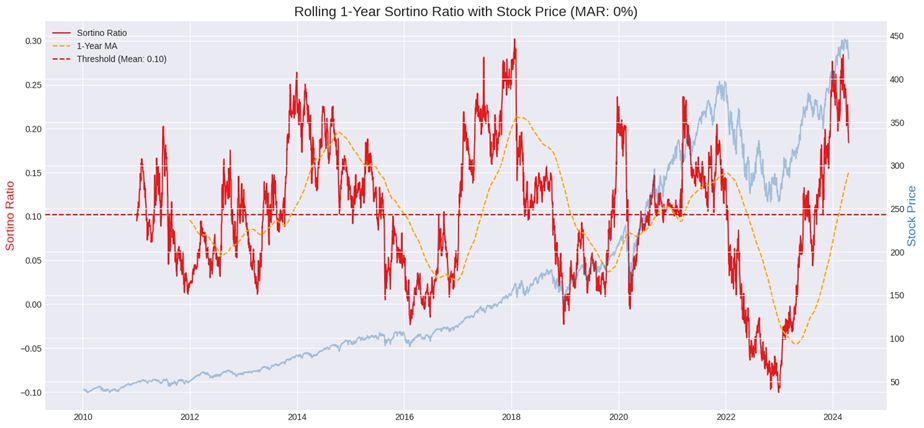
Ví dụ Phân tích tỷ lệ Sortino hàng năm của Visa bằng Python

Tỷ lệ Sharpe và Tỷ lệ Sortino đã trở nên thiết yếu để tối ưu hóa chiến lược đầu tư. Các phương pháp này không chỉ giúp các nhà đầu tư đánh giá hiệu quả rủi ro/lợi nhuận của từng khoản đầu tư một cách khoa học mà còn cung cấp những cái nhìn sâu sắc về khả năng tổng quát của các chiến lược đầu tư trong các điều kiện của thị trường. Bằng việc hiểu rõ và áp dụng linh hoạt những chỉ số này, nhà đầu tư có thể đưa ra các quyết định thông minh, giảm thiểu rủi ro và tăng cường tiềm năng sinh lời cho danh mục đầu tư của mình trong dài hạn.

Hẹn mọi người trong phần 2 về các tỷ lệ Calmar, Omega và Max Drawdown!

Link Google Colab: Tổng hợp các phương pháp đánh giá rủi ro và hiệu suất trong đầu tư